quarta-feira, 30 de outubro de 2013

Aula 11 - Exercicio

Nesta aula só fizemos um exercicio para revisar todo o conteudo:

1- Completar a tabela acima:

2- Calcular a média (X) e o desvio padrão
3- Desenvolver o histograma das freqüências absoluta e cumulativa, e o polígono das freqüências

Fonte: caderno de anotações

terça-feira, 29 de outubro de 2013

Aula 9 - Distribuição Uniforme, Normal/Gaussiana

Distribuição Uniforme

A distribuição uniforme é a mais simples distribuição contínua, entretanto uma das mais importantes e utilizadas dentro da teoria de probabilidade. A distribuição uniforme tem uma importante característica a qual a probabilidade de acontecer um fenômeno de mesmo comprimento é a mesma.

Definição 6.1.1: Uma variável aleatória $X$ tem distribuição Uniforme no intervalo $[a,b]$ se sua função densidade de probabilidade for dada por:

$f(x)=\left\{\begin{array}{l} \frac{1}{b-a}, \ \hbox{se} \ a\leq x\leq b;\\ 0, \ \hbox{caso contrário}\end{array}\right.$

O gráfico abaixo ilustra a função densidade da distribuição uniforme com parâmetros a=0 e b=1.

Exemplo: A ocorrência de panes em qualquer ponto de uma rede telefônica de $7$ km foi modelada por uma distribuição Uniforme no intervalo $[0, 7]$ . Qual é a probabilidade de que uma pane venha a ocorrer nos primeiros $800$ metros? E qual a probabilidade de que ocorra nos $3$ km centrais da rede?

A função densidade da distribuição Uniforme é dada por $f(x)=\frac{1}{7}$ se $0\leq x\leq 7$ e zero, caso contrário. Assim, a probabilidade de ocorrer pane nos primeiros 800 metros é

$\mathbb{P}\left(X\leq 0,8\right)=\int_0^{0,8} f(x)dx=\frac{0,8-0}{7}=0,1142.$

e a probabilidade de ocorrer pane nos 3 km centrais da rede é

$\mathbb{P}\left(2\leq X\leq 5\right)=\int_2^5f(x)dx=\mathbb{P}\left(X\leq 5\right)-\mathbb{P}\left(X\leq 2\right)=5/7-2/7\approx 0,4285.$

Distribuição Normal/Gaussiana

A distribuição normal é a mas importante distribuição estatística,
considerando a questão prática e teórica. Já vimos que esse tipo de distribuição apresenta-se em formato de sino, unimodal, simétrica em relação a sua média.
Considerando a probabilidade de ocorrência, a área sob sua curva soma 100%. Isso quer dizer que a probabilidade de uma observação assumir um valor entre dois pontos quaisquer é igual à área compreendida entre esses dois pontos.

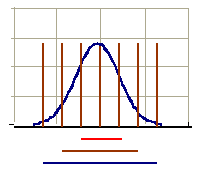
68,26% => 1 desvio
95,44% => 2 desvios
99,73% => 3 desvios

Na figura acima, tem as barras na cor marrom representando os desvios padrões. Quanto mais afastado do centro da curva normal, mais área compreendida abaixo da curva haverá. A um desvio padrão, temos 68,26% das observações contidas. A dois desvios padrões, possuímos 95,44% dos dados comprendidos e finalmente a três desvios, temos 99,73%. Podemos concluir que quanto maior a variablidade dos dados em relação à média, maior a probabilidade de encontrarmos o valor que buscamos embaixo da normal.
Propriedade 1:
"f(x) é simétrica em relação à origem, x = média = 0;
Propriedade 2:
"f(x) possui um máximo para z=0, e nesse caso sua ordenada vale 0,39;
Propriedade3:
"f(x) tende a zero quando x tende para + infinito ou - infinito;
Propriedade4:
"f(x) tem dois pontos de inflexão cujas abscissas valem média + DP e média - DP, ou quando z tem dois pontos de inflexão cujas abscissas valem +1 e -1.

Fonte: http://www.somatematica.com.br/estat/basica/normal.php

http://www.portalaction.com.br/content/61-distribui%C3%A7%C3%A3o-uniforme

Aula 8 - Amplitude Amostral

Amplitude de uma amostra (ou coleção) de dados de tipo quantitativo é a diferença entre o valor máximo e o valor mínimo da amostra

R = Máximo – Mínimo

A amplitude é a medida mais simples para medir a variabilidade ou dispersão dos dados.

Tem de se ter o devido cuidado na sua utilização, pois basta haver na amostra uma ou mais observações muito maiores ou muito menores que as restantes para que a amplitude não reflita a dispersão do conjunto dos dados por esta ser muito sensível a essa, ou essas,observações. Por exemplo, os dois conjuntos de dados representados a seguir,

11,21,51,71,81,922,32,52,68

122,544,55,566,477,58

têm a mesma amplitude, igual a 7, mas a sua variabilidade é muito diferente:

Amplitude

Amplitude Total: intervalo entre todas as classes, diferença entre o limite superior da última classe e o limite inferior da primeira classe.

Amplitude Amostral: intervalo entre o maior e o menor valor dos dados da amostra (ROL)

Amplitude de Classe: diferença entre o limite superior e o limite inferior de uma classe. Ex: 10 |— 20 a amplitude é: 20 – 10 = 10

Amplitude de Classes: maior valor menos o menor valor dividido pelo número de classes.

Fonte: http://notasdeaula.files.wordpress.com/2009/09/aula06-estatistica.pdf http://www.ferrari.pro.br/home/documents/FFerrari-Curso-Estatistica-Basica.pdf

domingo, 27 de outubro de 2013

Aula 7 - Frequência Relativa, Acumulada e Absoluta

Frequência Absoluta e Relativa

A Estatística é uma ferramenta matemática muito utilizada em vários setores da sociedade, organizando dados de pesquisas e apresentando informações claras e objetivas. Iremos através de um exemplo construir uma tabela de frequência absoluta e frequência relativa de uma variável.

Exemplo
Às pessoas presentes em um evento automobilístico foi feita a seguinte pergunta: Qual a sua marca de carro preferida?

Pedro: Ford	Bruna: Peugeot	Anete: Ford	Paulo: Peugeot	Célio: Volks	Manoel: GM
Carlos: GM	Fred: Volks	Sérgio: Fiat	Gilson: GM	Rui: Fiat	Cláudia: Volks
Antônio : Fiat	Márcio: Volks	Marcelo: GM	Ana: Nissan	Geraldo: Volks	Rita: Ford
Pedro: Ford	Alicia: Renault	Meire: GM	Flávio: Peugeot	Lia: GM	Fabiano: Renault

Construindo uma tabela para melhor dispor os dados:

Marcas	Frequência Absoluta (FA)	Frequência Relativa (FR)
Ford	4	16,7%
Fiat	3	12,5%
GM	6	25%
Nissan	1	4,2%
Peugeot	3	12,5%
Renault	2	8,3%
Volks	5	20,8%
Total	24	100%

Frequência absoluta: quantas vezes cada marca de automóvel foi citada.

Frequência relativa: é dada em porcentagem. A marca Ford tem frequência relativa 4 em 24 ou 4/24 ou ~0,166 ou 16,66% ou 16,7%.

Frequência Acumulada

Dada a distribuição de freqüências abaixo, representativa de uma população de 50.000 pessoas, construir a distribuição de freqüências acumulada (e apenas ela) obedecendo às Normas de Apresentação Tabular.

Fonte:

http://www.tutorbrasil.com.br/forum/matematica-ensino-superior/estatistica-frequencia-absoluta-acumulada-t19364.html

http://www.brasilescola.com/matematica/aplicacao-estatistica-frequencia-absoluta-frequencia-.htm

Bandas de Bollinger

O que seria Bandas de Bollinger ?

Criado pelo grande professor John Bollinger.

As bandas Bollinger são ferramentas de análise técnica criadas por John Bollinger no início dos anos 80. Este indicador possui uma forte relação com a volatilidade, possibilitando, assim, a sua comparação com os níveis de preços num determinado período de tempo. O maior objetivo das bandas Bollinger é fornecer uma idéia relativa de alto e baixo. Por definição, os preços são altos na linha (banda) superior e baixos na linha (banda) inferior.

As bandas Bollinger são constituídas por um conjunto de três curvas desenhadas em relação aos preços. Elas são traçadas a partir de uma determinada distância de uma média móvel. A banda intermediária é uma medida de tendência intermediária, geralmente uma média móvel simples, que serve como base para as bandas inferiores e superiores. O intervalo entre as bandas superiores, intermediárias e inferiores é determinado pela volatilidade, geralmente o desvio padrão da mesma data que foi utilizada pela média. Assim, quanto maior a volatilidade de um ativo maior seu desvio padrão.

As Bandas de Bollinger consistem de:

Bandas Bollinger Intermediárias sendo uma N-período média móvel simples;

Bandas Bollinger Superiores sendo Bandas Bollinger Intermediárias + (K x N-período desvio padrão);

Bandas Bollinger Inferiores = Bandas Bollinger Intermediárias - (K x N-período desvio padrão).

Valores típicos para K e N são 2 e 20, respectivamente.

O uso das Bandas de Bollinger variam muito entre os investidores. Dessa forma, alguns deles compram quando o preço toca a banda Bollinger inferior e vendem quando o preço toca a média móvel no centro das bandas. Outros investidores compram quando o preço sobe acima da banda superior e o vendem quando o preço cai abaixo da banda inferior.

Frequentemente, quando as bandas de Bollinger se aproximam da média, o preço das ações de uma companhia sofrem consideráveis alterações. Assim, movimentos fora das bandas propõem a continuação da tendência. Altas e baixas fora das bandas, seguidas de altas e baixas dentro das bandas propõem uma reversão de tendência. Em fato, quando não há tendência definida, a regra é vender quando o preço ficar acima da banda superior e comprar quando o preço ficar abaixo da banda inferior.

Fonte: http://br.advfn.com/educacional/analise-tecnica/bandas-bollinger

https://www.google.com.br/search?q=john+bollinger&tbm=isch&tbo=u&source=univ&sa=X&ei=grptUuy8IaHE7Aadr4Ew&ved=0CC0QsAQ&biw=1366&bih=600#facrc=_&imgdii=_&imgrc=UqJ7HWllITVg7M%3A%3BRFSkeQ16JEbIEM%3Bhttp%253A%252F%252Fuser.tninet.se%252F~cpz942y%252Fimages%252Fjohn_bollinger.jpg%3Bhttp%253A%252F%252Fuser.tninet.se%252F~cpz942y%252Fglossary.htm%3B175%3B195

Aula 5 - Desvio Padrão e Mais

Entenda como funciona o Desvio Padrão:

Quanto foi a sua média de matemática no último bimestre? Um dos conceitos mais básicos e cotidianos da estatística, a média nada mais é que um valor que "representa" vários outros. Com os exemplos a seguir, você vai ver que é fácil.

Imagine que, no bimestre, João fez cinco atividades que valiam nota nas aulas de matemática. Ele começou bem, mas terminou o bimestre mal. Tirou as seguintes notas: 9, 7, 5, 3, 2.

Qual será a sua média no fim do bimestre?

Para facilitar os cálculos, vamos adotar o seguinte padrão: S é a soma das notas, e n é o número de notas que ele teve.

A média (M) será:

Note que a sua média não é igual a nenhuma das notas que ele tirou. É um número que mostra, mais ou menos, como João foi no bimestre.

Medidas de dispersão

Muitas vezes, a média não é suficiente para avaliar um conjunto de dados. Por exemplo, quando se fala em um grupo de mulheres com idade média de 18 anos. Esse dado, sozinho, não significa muito: pode ser que no grupo, muitas mulheres tenham 38 anos, e outras tantas sejam menininhas de dois!

É importante, então, conhecer outra medida, a de que diferença (dispersão) existe entre a média e os valores do conjunto.

Voltando ao exemplo das notas de João, podemos calcular o desvio, que é a diferença de cada nota em relação à média:

Notas	Média	Desvio
9	5,2	3,8
7	5,2	1,8
5	5,2	- 0,2
3	5,2	- 2,2
2	5,2	- 3,2

Outro dado importante em estatística é obtido pela soma dos desvios ao quadrado. Cada desvio é elevado ao quadrado e, em seguida, somados:

Valores	Média	Desvio	Quadrado dos desvios
9	5,2	3,8	14,44
7	5,2	1,8	3,24
5	5,2	- 0,2	0,04
3	5,2	- 2,2	4,84
2	5,2	- 3,2	10,24
Soma dos quadrados dos desvios			32,8

A soma dos quadrados dos desvios dividida pelo número de ocorrências é chamada de variância.

Logo:

Outro valor que pode ser obtido a partir da média e da variância é o desvio padrão. Como os desvios foram elevados ao quadrado, deve-se tirar a raiz quadrada da variância e achar o desvio padrão:

Só para se ter uma idéia melhor do que significa o desvio padrão veja o seguinte exemplo:

Notas: (9, 9, 9, 1, 1, 1)

A média será:

E o desvio padrão será Dp = 4 (tente calculá-lo por conta própria).

Note que, apesar de esse aluno ter tido média 5, seu desempenho foi muito irregular (variou de 4 pontos! 5+4 =9 e 5-4 = 1), o que não é tão bom assim.

No exemplo anterior pode-se interpretar que as notas, no geral, variaram entre (5,2 + 2,56) = 7,76 e (5,2 - 2,56) = 2,64 , ou seja, Joãozinho teve desempenho mais regular que esse outro aluno.

Fonte: http://educacao.uol.com.br/matematica/media-desvio-padrao-e-variancia-nocoes-de-estatistica.jhtm

Ondas de Elliott

O que é a Teoria das Ondas de Elliott ?

Neste artigo você irá entender o que é a teoria das Ondas de Elliott, e como ela pode ser utilizada na análise técnica.

Atualmente, tanto para quem utiliza a Análise Fundamentalista quanto a Análise Técnica, é praticamente lugar comum falar que o mercado se movimenta em ciclos de alta e de baixa. Porém, foi Ralph Nelson Elliott o gênio que, entre as décadas de 30 e 40 do século XX, conseguiu demonstrar e provar graficamente que os movimentos dos preços se comportavam de formas cíclicas formando padrões geométricos, os quais eram gerados pelo comportamento do emocional de massa no mercado financeiro.

Representação real de um ciclo da Teoria das Ondas de Elliott:

Sua base de raciocínio é a de que a emoção surge primeiro que a ação. Por isso, a representação gráfica de uma série histórica de cotações de um ativo nada mais é do que a oscilação de humor do coletivo numa tentativa desesperada de encontrar sua precificação.

Segundo Elliott, o público age de forma emocional, subjetiva e impulsiva, tomando decisões em condições de ignorância e incerteza, e, na maioria das vezes, assumindo a chamada "atitude manada".

Com o propósito de quantificar a psicologia humana associada às oscilações dos preços, Elliott catalogou diversos desses padrões gráficos criando específicas regras, originando assim o Princípio das Ondas de Elliott ou, simplesmente, Teoria de Elliott.

Logo abaixo, de forma resumida, segue o padrão geométrico de um ciclo que Ralph Elliott identificou. Note que a representação gráfica é mais que um simples padrão, é uma forma de se mapear a evolução do preço até o momento presente, a fim de vislumbrar cenários futuros.

Representação teórica padrão:

A identificação dos padrões gráficos permitiu que Elliott conseguisse encontrar as "formas" existentes no mercado de capitais, porém faltava uma ferramenta que lhe auxiliasse medir essas mesmas formas. Então Elliott recorreu à matemática e lá encontrou uma importante proporção chamada de Número de Ouro (=1,618) que foi extraída da seqüência de números de Fibonacci, a qual possui fortes correlações com o seu princípio.

Para este estudioso, os ciclos têm características definidas e a compreensão de sua Teoria permite que o investidor possa antecipar com certa precisão grandes reversões de tendência tanto de índices, ações, derivativos, commodities ou moedas, e, assim, aproveitar os bons movimentos de alta ou de baixa do mercado.

Fonte: http://www.elliottbrasil.com/teoriadeelliott.php

Sequência Fibonacci

O que é a sequência de Fibonacci ?

É uma sucessão de números que, misteriosamente, aparece em muitos fenômenos da natureza. Descrita no final do século 12 pelo italiano Leonardo Fibonacci, ela é infinita e começa com 0 e 1. Os números seguintes são sempre a soma dos dois números anteriores. Portanto, depois de 0 e 1, vêm 1, 2, 3, 5, 8, 13, 21, 34…

Ao transformar esses números em quadrados e dispô-los de maneira geométrica, é possível traçar uma espiral perfeita, que também aparece em diversos organismos vivos. Outra curiosidade é que os termos da sequência também estabelecem a chamada “proporção áurea”, muito usada na arte, na arquitetura e no design por ser considerada agradável aos olhos. Seu valor é de 1,618 e, quanto mais você avança na sequência de Fibonacci, mais a divisão entre um termo e seu antecessor se aproxima desse número.

GIRANDO, GIRANDO

Exemplos na natureza em que a sequência ou a espiral de Fibonacci aparece

CONCHA DO CARAMUJO

Cada novo pedacinho tem a dimensão da somados dois antecessores

CAMALEÃO

Contraído, seu rabo é uma das representações mais perfeitas da espiral de Fibonacci

ELEFANTE

Se suas presas de marfim crescessem sem parar, ao final do processo, adivinhe qual seria o formato?

GIRASSOL

Suas sementes preenchem o miolo dispostas em dois conjuntos de espirais: geralmente, 21 no sentido horário e 34 no anti-horário

PINHA

As sementes crescem e se organizam em duas espirais que lembram a de Fibonacci: oito irradiando no sentido horário e 13 no anti-horário

POEMA CONTADINHO

Acharam o “número de ouro” até na razão entre as estrofes maiores e menores da Ilíada, épico de Homero sobre os últimos dias da Guerra de Troia

A BELEZA DESCRITA EM NÚMEROS

A “Proporção de ouro” aparece tanto em seres vivos quanto em criações humanas. Na matemática, a razão dourada é representada pela letra grega phi: φ

PARTENON

Os gregos já conheciam a proporção, embora não a fórmula para defini-la. A largura e a altura da fachada deste templo do século V a.C. estão na proporção de 1 para 1,618

ARTES

Esse recurso matemático também foi uma das principais marcas do Renascimento. A Mona Lisa, de Leonardo da Vinci, usa a razão na relação entre tronco e cabeça e entre elementos do rosto

AS GRANDES PIRÂMIDES

Mais um mistério: cada bloco é 1,618 vezes maior que o bloco do nível imediatamente acima. Em algumas, as câmaras internas têm comprimento 1,618 vezes maior que sua largura

OBJETOS DO COTIDIANO

Vários formatos de cartão de crédito já foram testados. O que se sagrou favorito do público têm laterais na razão de ouro. Fotos e jornais também costumam adotá-la

ROSTO

Dizem que, nas faces consideradas mais harmoniosas, a divisão da distância entre o centro da boca e o “terceiro olho” pela distância entre esse ponto e uma das pupilas bate no 1,618

CORPO

Se um humano “mediano” dividir sua altura pela distância entre o umbigo e a cabeça, o resultado será algo em torno de 1,618

MÃOS

Com exceção do dedão, em todos os outros dedos as articulações se relacionam na razão áurea

Fonte: http://mundoestranho.abril.com.br/materia/o-que-e-a-sequencia-de-fibonacci

Triângulo de Pascal

O Triângulo de Pascal é muito utilizado em Análise Combinatória, recebe esse nome devido ao matemático Blaise Pascal que descobriu a maioria de suas propriedades. O triângulo de Pascal é um triângulo aritmético formado por números que têm diversas relações entre si.

Cada linha representa os números binomiais na expansão de (x+y)n, n≥0. Por exemplo: (x+y)3=1.x3 + 3x2y + 3xy2 + 1.y3 e na quarta linha temos 1 3 3 1.

NOTA: Considera-se que o topo do triângulo corresponde à linha 0, coluna 0.

Apresentando a fórmula matemática para esta propriedade:

sendo n o número de linhas e k o número de colunas dessa linha onde o número está (não se conta com o topo do triângulo, pois numa sucessão definida por recorrência tem que existir uma condição inicial, tal é 1).

Tal fórmula prova-se por indução matemática em n.

Fonte: http://whttp://www.infoescola.com/combinatoria/triangulo-de-pascal/

www.educ.fc.ul.pt/docentes/opombo/seminario/pasca_l/pascal.htm

segunda-feira, 14 de outubro de 2013

QI - Quoeficiente de Inteligência

O que são Testes de QI ?

São testes que visam avaliar a capacidade cognitiva de uma pessoa em relação a sua faixa etária. Nesses testes, quase sempre são empregadas medidas como: tempo médio de solução dos problemas, quantidade de erros/acertos, etc.

A sigla QI quer dizer Quoeficiente de Inteligência e foi criada por Wilhelm Stern, em 1912. Ele também introduziu os termos "idade mental" e "idade cronológica".

Correlação com Sucesso

O QI é estudado porque ele se correlaciona muito bem com sucesso medido em uma variedade de eventos na vida de um sujeito. Pessoas com alto QI geralmente tem altos graus de educação (mestres, doutores e pós-doutores), salários elevados e saúde ótima. Por outro lado, a sensação de felicidade pessoal não parece estar ligada com a inteligência do sujeito.

Como é classificado o QI ?

A classificação clássica proposta por Lewis Terman é:

QI acima de 140: Genialidade
121 - 140: Inteligência muito acima da média
110 - 120: Inteligência acima da média
90 - 109: Inteligência normal (ou média)
90 - 109: Inteligência normal (ou média)
80 - 89: Embotamento
70 - 79: Limítrofe
50 - 69: Cretino

A onde surgiu o primeiro teste de QI ?

O primeiro teste surgiu na China há mais de 1500 anos atrás, mas somente no início do século XX, na França, eles começaram a ter significado científico.

Entenda melhor neste vídeo abaixo, desde como monta e resolve um teste de QI.

Fontes:

http://www.testesdeqi.com.br/

http://www.youtube.com/watch?v=QltOLLo--jU

3ª Aula - O Problema de Monty Hall

Conhecendo o Jogo

A maneira que você joga determina suas chances de vencer, mas você pode se surpreender ao saber qual a melhor estratégia.

Um apresentador de um jogo televisivo norte-americano chamado Let’s Make a Deal, que foi ao ar há alguns anos. Em um dos jogos, Monty apresentava aos participantes três portas.

Atrás de uma delas há um carro. Atrás das outras duas, nada. Monty sabe o que tem atrás de cada porta, mas você não sabe.

Aplicando o Jogo

O jogo é disputado em três etapas:

Você escolhe uma porta.
Monty abre uma das duas outras portas que você não escolheu, revelando um espaço vazio (ele nunca abre a porta que tem o carro).
Agora você tem a escolha de ou permanecer com a porta que escolheu na etapa 1 ou trocar para a outra porta, que ainda está fechada.


	Digamos que você escolha a porta A. Monty abre	uma das outras duas portas, como por exemplo a B.


		Agora você tem a opção de trocar para a porta C ou permanecer com	sua escolha original, A.

Trocando você pode se dar bem, ou não !



O que você faz ? Fica com sua escolha original ou troca depois que Monty abre a porta ? .

Veja no vídeo abaixo uma explicação simplificada porém completa :

Fontes:

http://www.planetseed.com/pt-br/mathpuzzles/o-problema-de-monty-hall

http://www.youtube.com/watch?v=Hh7pDPnKK-4